Simple Harmonic Motion
Oscillations occur when a system is disturbed from a position of stable equilibrium. Examples include a swinging pendulum or a plucked musical instrument.
An import type of oscillatory motion is Simple Harmonic Motion, in that when an object is displaced from an quilibrium position, for example a mass on a spring it exerts a force –kx, as given by Hooke’s Law, where k is the spring constant.
When this is applied to Newton’s Second law it can be proved that the acceleration of an object is proportional to the displacement and oppositely directed, and will move with Simple Harmonic Motion. Click here to see how this can be proved.
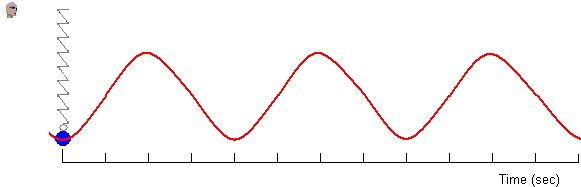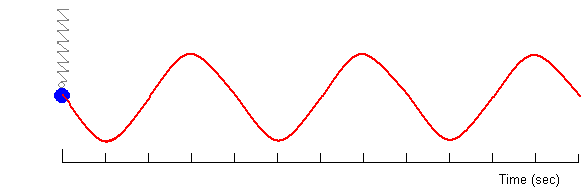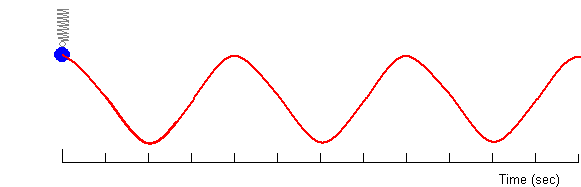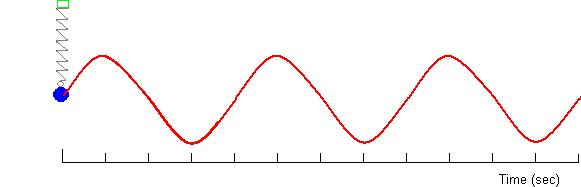 The experimential representation of Simple Harmonic Motion seen here shows we can obtain a x verses t relation ship for a mass on a spring. The general equationl for the curve is:
The experimential representation of Simple Harmonic Motion seen here shows we can obtain a x verses t relation ship for a mass on a spring. The general equationl for the curve is:
In the equation the Amplitude (A) is the maximum displacement. The phase and phase constant depend on the number of oscillation systems. If there is only one system the Phase Constant = 0, if there are more than one systems with the same amplitude but oscillating at different frequencies there is said to be in different phase.
We can also derive a velocity and acceleration of the oscillation, click here to see the method.