Richard Hobbs1 and Helmut Jakubowicz2
1Department of Earth Sciences, University of Cambridge, Bullard Laboratories, Madingley Road, Cambridge, UK
2Veritas
DGC Ltd, Crompton Way, Manor Royal Estate, Crawley, West Sussex, UK
Introduction
The quality and reliability of seismic data is controlled by a number of factors, but is ultimately constrained by the nature of the seismic source. As a result, it is desirable to determine the source output (the "signature") and correct for its effect using deconvolution (see, for example, Ziolkowski, 1982, and Ziolkowski, 1991). Indeed, signature deconvolution is not only a necessary prerequisite for maximising the temporal, vertical and lateral resolution of seismic data, but is also important for reconciling data in time-lapse studies, the accurate determination of amplitude variations with offset, and wave-equation multiple removal and inversion schemes.
Unfortunately, whereas signature correction is, in principle, a relatively simple procedure, accurate signature determination is not. In particular, the source output can vary from shot to shot, and it is therefore desirable to measure the signature continuously during data acquisition. However, with the exception of recordings obtained at depth in wells or with hydrophones in deep water, current approaches to signature measurement (for example, the methods of Ziolkowski, Parkes, Hatton and Haugland, 1982, and Safar, 1998) use near-field recordings of individual guns within an airgun array to synthesise the far-field signature. Thus, these techniques not only require a significant additional effort in deploying large numbers of near-field hydrophones, but provide results that are sensitive to the assumed behaviour of the gun interactions, as well as the geometry and details of the surface reflections used for the far-field conversion (Safar, 1999).
In
this paper we revisit a method of signature measurement for marine seismic
data proposed by Newman (1985). This technique uses a calibration source
together with a single near-field recording to obtain a reference dataset
(i.e. earth impulse response), which is in turn used to extract the signature
of the primary source from the main recordings. In particular, although
this approach does share some characteristics of other near-field measurement
techniques, it requires significantly fewer measurements, calculations
and assumptions than alternative approaches, and could provide a simple
solution to the vexing task of marine source signature determination.
Background
Newman's method consists of recording the near-field signature and data from an individual (point) reference source in conjunction with the data from the main array. In practise, this is achieved by firing the reference source ahead of the main array (typically with a known delay of one or two seconds), and recording the results together with the desired data as a single record. The near-field recording is then converted to the far-field signature using a deterministic filter that corrects for the surface ghost, and the result is then used to deconvolve the corresponding data obtained from the reference gun. Finally, the results of this procedure are used to determine the signature implicit in the main recording, and the resulting signature then used in conjunction with the main data as appropriate. Indeed, the far-field conversion can incorporate directivity effects due to ghosting, hence the method can be extended to provide simple estimates of angular variations in the signature of the main array.
In practise, Newman's method is relatively simple to implement, and offers a number of advantages over other techniques. For example, because the reference data are recorded through the same equipment as the actual recordings from the main array, the response of the streamer and instruments are removed from the inferred signature. Similarly, assumptions that the sea conditions do not change between the times at which the reference and actual data are acquired, the method also compensates for any variation in ghosting effects along the source array. Finally, the method makes no assumptions regarding the interaction between individual airguns, and can therefore be used in conjunction with any array geometry.
Despite
its simplicity and strengths, Newman's method is also vulnerable to some
problems. For example, the far-field conversion is actually the same as
that implicit in other measurement schemes, and therefore shares the sensitivity
of those methods to errors in the geometry and presumed reflection behaviour
of the surface. In addition, weaknesses in the spectrum of the reference
source generate weaknesses at the corresponding frequencies in the signature
estimate. As a result, the reference signature must be relatively broad
band, and ordinary airguns are therefore unsuitable for this purpose because
of bubbling. Indeed, initial trials of Newman's method used a watergun
as a reference (Newman, 1985), although detailed results of these experiments
were never presented, and it appears that this implementation was "operationally
unsuccessful" (Safar, 1998).
Marine source signature measurement
Implementation
We have recently performed a new test of Newman's method in conjunction with a deep-regional, combined-surface seismic and OBS survey. Specifically, we used a "G.1. gun" (Pascouet, 1991) as the reference source to reduce bubbling. This device has two chambers, the second of which is fired slightly later than the first in order to attenuate the bubble pulse generated by the first chamber, and thereby generates a signature that is relatively broad band. The G.1. gun was deployed at the front of the main array, and monitored by hydrophones at 1 m, and 2 m above it (two hydrophones were used to provide redundancy in the measurements, although only one is required for the application of the method). The main array itself was designed to optimise penetration, had a total volume of 8910 cu ins, and was operated at a nominal depth of 10 m. The reference gun was fired two seconds ahead of the main array, and recordings were made for total of 24 seconds. The streamer was configured with 25 m groups, had a total length of 10 km, and was deployed at a depth 18 m.
Results
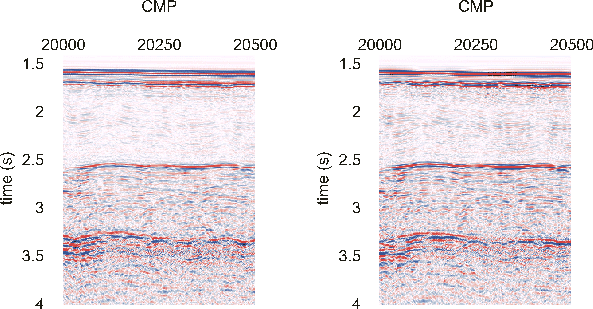
Figure
1 shows a shot record from the survey both with and without automatic gain
control. It can be seen that the energy of the reference source is sufficiently
weak to ensure that the main recording remains uncontaminated, yet that
it sufficiently strong to provide a useful recording in its own right.
Although the first two seconds of the recording (which correspond to the
reference data), show substantial evidence of residual bubbling, the near-field
recording at lm shows that energy is present at all frequencies within
the desired bandwidth (frequencies up to 125Hz). Further, careful filtering
of the reference gun data is required to suppress the direct arrival from
the main air-gun array at near offsets prior to using the data to estimate
the source signature.

(a)
(b)
Figure
1. A raw shot gather (a) without AGC, (b) with AGC. The single G.I. gun
reference source is fired 2 seconds before the main array.
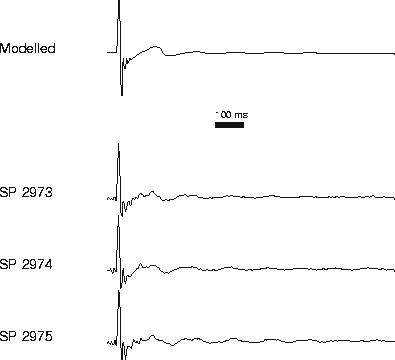
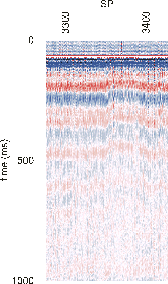
Figure 2 shows signatures estimated from the data shown in Figures 1 using Newman's technique. The estimated signature shares many of the features in the modelled signature, although it also contains significant differences due to deviations in the array performance introduced by weather conditions at the time of acquisition. Figure 3 shows the variation in gun signature for 150 sequential shots again shot-to-shot variability can be seen with a more systematic reduction in bubble pulse period between SP 3350 and 3400 that can be linked to a change in air pressure that was noted by the observers during acquisition.
|
Figure 2. Comparison between the expected
notional source function (Modelled)and those derived from the real data
using Newman's method for 3 consecutive shot points. Though there
is good agreement in the overall shape there are significant shot-to-shot
variations.
|
Figure 3. A series of notional source functions
derived from the seismic data showing a
change
in the bubble period between SP 3350 &
3400. The
cause of this change is noted in the Observer
Logs
as a reduction in air pressure.
|
(a)
(b)
Figure
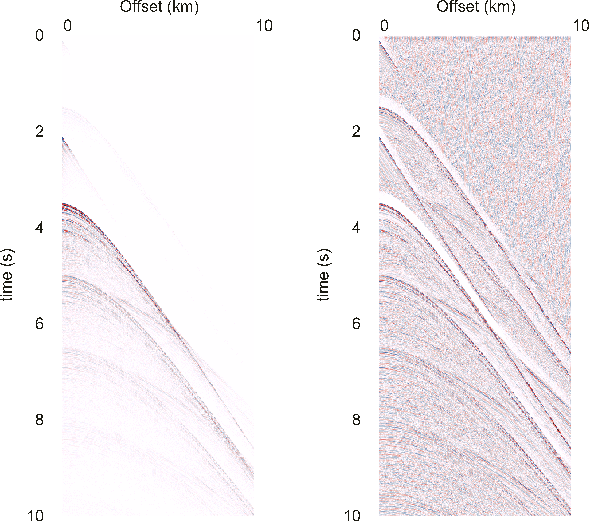
4. (a) Stacked section processed using the single modelled source signature;
(b) stacked section processed using the shot-by-shot derived source signatures.
We
stacked the data after deconvolution using both the single modelled signature
and the notional source signatures that we derived from the data. When
compared with the stack using the derived signatures (Fig. 4(b)), the stack
that has been processed with the modelled signature (Fig. 4(a)) has less
definition in the near-surface, also the reflection from the basalt at
3.3 s is less coherent and there is a vertical discontinuity at CMP 20200.
All these aspects are addressed by using the derived signature yielding
an improved stack.
Conclusions
We have conducted a new test of Newman's marine source signature measurement method using a G. 1. gun as the reference source. The results show that this approach does offer promise for providing shot-to-shot measurements of marine source signatures, and that these can be exploited to enhance the resolution of the corresponding data. Processing with a notional source is robust as it is not prone to instabilities caused by errors in modelling the surface ghosts at both the shot and receiver. However, the effects of the ghosts needs to be addressed and further analysis of the surface seismic data acquired during this survey is currently in progress, and the results will be described in the oral presentation of this talk.
Acknowledgements
The authors wish to thank Sodera for their assistance in providing the G.1. gun, and the crew of the M. V. Veritas Viking 11 for their efforts during the experiment. We are also grateful to Graeme Stewart who worked on this topic during his M.Sc. studies at the University of Birmingham, and to the members of the Atlantic Margin Project (Amerada Hess, BP Amoco, Conoco, Elf, Lasmo, Mobil, Saga, Shell, Statoil and Total) for permission to publish this work.
References
Newman, P., 1985, Continuous calibration of marine seismic sources, Geophys. Prosp., 33, 224-232.
Pascouet, A., 1991, Something new under the water: The bubbleless air gun: The Leading Edge, 10, no. 11, 79-81
Safar, M., 1998, A new method of marine seismic source estimation from near field measurements, Extended
Safar, M., 1999, On the improvement and quality control of the TRISOR source signature estimator, Extended
Ziolkowski, A., 1982, Further thoughts on Popperian geophysics - The example of deconvolution, Geophys.
Ziolkowski, A., Parkes, G., Hatton, L. and Haugland, T., 1982, The signature of an air-gun array - Computation
Ziolkowski, A., 1991, Why don't we measure seismic signatures?, Geophysics, 56, 190-201.